De wet van Ohm voor een volledige keten en voor een deel van een keten: mogelijkheden voor het schrijven van de formule, beschrijving en uitleg
Er is geen manier voor een professionele elektricien of elektronicaspecialist om de wet van Ohm te omzeilen in zijn eigen activiteiten, door problemen op te lossen die verband houden met het opzetten, afstellen en repareren van elektronische en elektrische circuits.
Eigenlijk moet iedereen deze wet begrijpen. Omdat iedereen in het dagelijks leven met elektriciteit te maken heeft.
En hoewel de wet van de Duitse natuurkundige Ohm in het leerplan van de middelbare school is opgenomen, wordt deze in de praktijk niet altijd tijdig bestudeerd. Daarom zullen we in ons materiaal een dergelijk relevant onderwerp voor het leven overwegen en de opties voor het schrijven van de formule begrijpen.
De inhoud van het artikel:
Enkele sectie en compleet elektrisch circuit
Als we een elektrisch circuit beschouwen vanuit het oogpunt van toepassing van de wet van Ohm op een circuit, moeten twee mogelijke berekeningsopties worden opgemerkt: voor een afzonderlijke sectie en voor een volwaardig circuit.
Berekening van de stroom van een elektrisch circuitgedeelte
Een deel van een elektrisch circuit wordt in de regel beschouwd als het deel van het circuit dat de bron van EMF uitsluit, omdat het extra interne weerstand heeft.
Daarom ziet de berekeningsformule er in dit geval eenvoudig uit:
ik = U/R,
Waar respectievelijk:
- I – huidige sterkte;
- U – aangelegde spanning;
- R - weerstand.
De interpretatie van de formule is eenvoudig: de stroom die door een bepaald gedeelte van het circuit vloeit, is evenredig met de spanning die erop wordt toegepast, en de weerstand is omgekeerd evenredig.
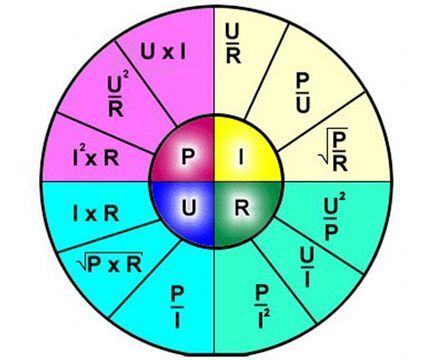
De formule beschrijft dus duidelijk de afhankelijkheid van de stroom door een afzonderlijk gedeelte van het elektrische circuit ten opzichte van bepaalde spannings- en weerstandswaarden.
De formule is handig om bijvoorbeeld te gebruiken bij het berekenen van de parameters van de weerstand die in het circuit moet worden gesoldeerd als de spanning en stroom worden gegeven.
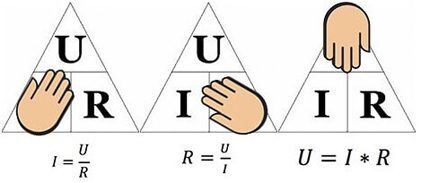
De bovenstaande figuur helpt bijvoorbeeld bij het bepalen van de stroom die door een weerstand van 10 ohm vloeit waarop een spanning van 12 volt wordt toegepast. Als we de waarden vervangen, vinden we – I = 12 / 10 = 1,2 ampère.
De problemen bij het vinden van weerstand (wanneer de stroom en spanning bekend zijn) of spanning (wanneer de spanning en stroom bekend zijn) worden op een vergelijkbare manier opgelost.
Zo kunt u altijd de gewenste bedrijfsspanning, de benodigde stroomsterkte en het optimale weerstandselement selecteren.
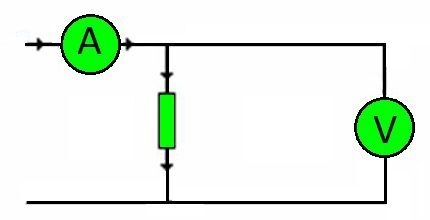
Trouwens, de verbindingsdraden van elk circuit zijn weerstanden. De hoeveelheid belasting die ze moeten dragen, wordt bepaald door de spanning.
Dienovereenkomstig wordt het, wederom met behulp van de wet van Ohm, mogelijk om nauwkeurig de vereiste geleiderdoorsnede te selecteren, afhankelijk van het kernmateriaal.
We hebben gedetailleerde instructies op onze website berekening van de kabeldoorsnede qua kracht en stroom.
Rekenmogelijkheid voor een complete keten
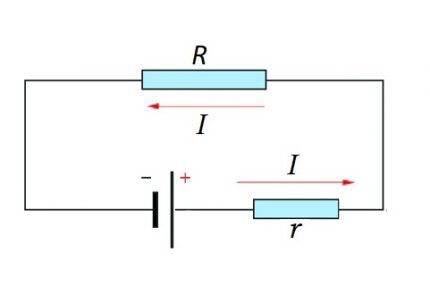
Een compleet circuit bestaat uit een sectie (secties) en een bron van EMF. Dat wil zeggen dat de interne weerstand van de EMF-bron in feite wordt toegevoegd aan de bestaande weerstandscomponent van de circuitsectie.
Daarom is het logisch om de bovenstaande formule enigszins te wijzigen:
ik = U / (R + r)
Natuurlijk kan de waarde van de interne weerstand van de EMF volgens de wet van Ohm voor een compleet elektrisch circuit als verwaarloosbaar worden beschouwd, hoewel deze weerstandswaarde grotendeels afhangt van de structuur van de EMF-bron.
Bij het berekenen van complexe elektronische circuits, elektrische circuits met veel geleiders, is de aanwezigheid van extra weerstand echter een belangrijke factor.
Zowel voor een deel van een circuit als voor een compleet circuit moet rekening worden gehouden met het natuurlijke moment: het gebruik van constante of variabele stroom.
Als de hierboven genoemde punten, kenmerkend voor de wet van Ohm, worden beschouwd vanuit het oogpunt van het gebruik van gelijkstroom, ziet alles er bij wisselstroom enigszins anders uit.
Overweging van het effect van de wet op een variabele hoeveelheid
Het concept van “weerstand” tegen de omstandigheden van het passeren van wisselstroom moet meer worden beschouwd als het concept van “impedantie”. Dit verwijst naar de combinatie van een ohmse belasting (Ra) en een reactieve weerstandsbelasting (Rr).
Dergelijke verschijnselen worden veroorzaakt door de parameters van inductieve elementen en de schakelwetten in relatie tot een variabele spanningswaarde - een sinusoïdale stroomwaarde.
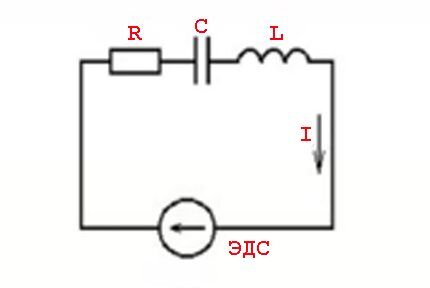
Met andere woorden, er is een effect van stroomwaarden die leiden (vertraging) van spanningswaarden, wat gepaard gaat met het verschijnen van actieve (resistieve) en reactieve (inductieve of capacitieve) krachten.
Dergelijke verschijnselen worden berekend met behulp van de formule:
Z=U/I of Z = R + J * (XL -XC)
Waar: Z – impedantie; R – actieve belasting; XL , XC – inductieve en capacitieve belasting; J - coëfficiënt.
Seriële en parallelle verbinding van elementen
Voor elementen van een elektrisch circuit (gedeelte van een circuit) is een karakteristiek punt een seriële of parallelle verbinding.
Dienovereenkomstig gaat elk type verbinding gepaard met een ander stroom- en spanningspatroon.In dit opzicht wordt de wet van Ohm ook anders toegepast, afhankelijk van de mogelijkheid om elementen op te nemen.
Circuit van in serie geschakelde weerstandselementen
Met betrekking tot een serieschakeling (een deel van een circuit met twee componenten) wordt de volgende formulering gebruikt:
- ik = ik1 =Ik2 ;
- U = U1 +U2 ;
- R = R1 + R2
Deze formulering laat duidelijk zien dat, ongeacht het aantal in serie geschakelde weerstandscomponenten, de stroom die door een deel van het circuit vloeit, niet in waarde verandert.
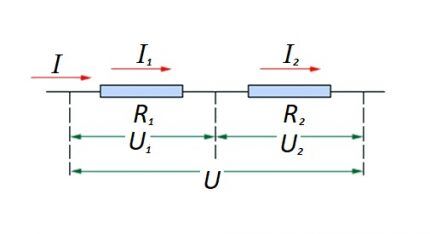
De grootte van de spanning die wordt aangelegd op de effectieve weerstandscomponenten van het circuit is de som en somt de waarde van de emf-bron op.
In dit geval is de spanning op elke afzonderlijke component gelijk aan: Ux = ik * Rx.
De totale weerstand moet worden beschouwd als de som van de waarden van alle resistieve componenten in het circuit.
Circuit van parallel verbonden weerstandselementen
In het geval dat er een parallelle verbinding is van resistieve componenten, wordt de volgende formulering als eerlijk beschouwd in relatie tot de wet van de Duitse natuurkundige Ohm:
- ik = ik1 +Ik2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1/R2 + …
Opties voor het maken van circuitsecties van een "gemengd" type, wanneer parallelle en seriële verbindingen worden gebruikt, zijn niet uitgesloten.
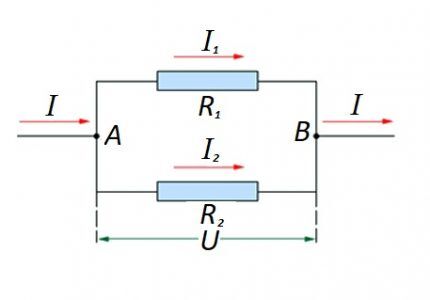
Voor dergelijke opties wordt de berekening meestal uitgevoerd door eerst de weerstandswaarde van de parallelle verbinding te berekenen. Vervolgens wordt de waarde van de in serie geschakelde weerstand opgeteld bij het verkregen resultaat.
Integrale en differentiële vormen van het recht
Alle bovenstaande punten met berekeningen zijn van toepassing op omstandigheden waarin geleiders met een zogezegd "homogene" structuur worden gebruikt in elektrische circuits.
Ondertussen heeft men in de praktijk vaak te maken met de constructie van schema's, waarbij de structuur van de geleiders in verschillende secties verandert. Er worden bijvoorbeeld draden met een grotere doorsnede gebruikt of, omgekeerd, een kleinere, gemaakt van verschillende materialen.
Om met dergelijke verschillen rekening te houden, is er een variatie op de zogenaamde ‘differentiaal-integrale wet van Ohm’. Voor een oneindig kleine geleider wordt het stroomdichtheidsniveau berekend afhankelijk van de spanning en de geleidbaarheidswaarde.
Voor de differentiaalberekening wordt de volgende formule gebruikt: J = ό * E
Voor de integraalberekening is de formulering dus: ik * R = φ1 – φ2 + έ
Deze voorbeelden liggen echter eerder dichter bij de school voor hogere wiskunde en worden niet daadwerkelijk gebruikt in de echte praktijk van een eenvoudige elektricien.
Conclusies en nuttige video over het onderwerp
Een gedetailleerde analyse van de wet van Ohm in de onderstaande video zal helpen om eindelijk de kennis in deze richting te consolideren.
Een unieke videoles versterkt de theoretische schriftelijke presentatie kwalitatief:
Het werk van een elektricien of de activiteit van een elektronica-ingenieur is integraal verbonden met momenten waarop men de wet van Georg Ohm daadwerkelijk in praktijk moet brengen. Dit zijn enkele waarheden die elke professional zou moeten weten.
Uitgebreide kennis over dit onderwerp is niet vereist - het is voldoende om de drie belangrijkste variaties van de formulering te leren om deze met succes in de praktijk toe te passen.
Wilt u bovenstaand materiaal aanvullen met waardevol commentaar of uw mening geven? Schrijf opmerkingen in het blok onder het artikel. Als u vragen heeft, aarzel dan niet om deze aan onze experts te stellen.



